On survival analysis and KM plots

“cie la vie”

In the context of biomedical sciences, survival analysis is used to study the relationship between time and outcome. More broadly speaking, ‘How likely is a non-reversible process X to have happened within T time?’.

This process is usually presented using a Kaplan-Meier (KM) plot. This tutorial will cover plotting a KM plot programmatically on a synthetic dataset using the lifelines package in Python.

Prerequisite

• lifelines
• numpy
• pandas
• matplotlib

Installation

pip install lifelines

Usage

1. Import packages and initialise the Kaplan-Meier Fitter

    import pandas as pd
    import numpy as np
    from lifelines import KaplanMeierFitter
    from lifelines.statistics import logrank_test
    import matplotlib.pyplot as plt
    kmf = KaplanMeierFitter()
    np.random.seed(42) #set a seed for reproducibility
   

2. Define patient and group functions

   To begin with, define the studypatient class, with each patient carrying the status and group information.

    class studypatient:
        def __init__(self, group, status):
            self.group = group
            self.status = status
   

   Let’s also define two functions, each for the gorup of ‘control’ and ‘sick’ patients.

   For the control group, let’s say the probability of an event is a fixed 0.01 (1 in 100).

    def controlgroup(nsize, totaltime) -> pd.DataFrame:
        currenttime = 0
        df = pd.DataFrame(columns=['time', 'event', 'group'])
        groupname = 'control'
        patients = [studypatient(groupname, 0) for _ in range(nsize)]
   
        while currenttime < totaltime:
            for _, patient in enumerate(patients):
                if np.random.randint(1, 101) == 1: #hitting an event
                    if patient.status == 0: #check if patient have occured the event
                        patient.status = 1 #update patient status
                df = df._append({'time': currenttime, 'event': patient.status, 'group': groupname}, ignore_index=True)
            currenttime += 1
        return df
   

   For the sick group, let’s say the probability of an event is higher at 0.05 (1 in 20).

    def sickgroup(nsize, totaltime):
        currenttime = 0
        df = pd.DataFrame(columns=['time', 'event', 'group'])
        groupname = 'sick'
        patients = [studypatient(groupname, 0) for _ in range(nsize)]
   
        while currenttime < totaltime:
            for _, patient in enumerate(patients):
                if np.random.randint(1, 21) == 1: #hitting an event
                    if patient.status == 0: #check if patient have occured the event
                        patient.status = 1 #update patient status
                df = df._append({'time': currenttime, 'event': patient.status, 'group': groupname}, ignore_index=True)
            currenttime += 1
        return df
   

3. Initilize the data in the groups

   In this example, let’s do 100 patients in each group for 50 time units.

    controldf = controlgroup(100, 50)
    sickdf = sickgroup(100, 50)
    df = pd.concat([controldf, sickdf])
    df.head()
   

4. Plot the Kaplan-Meier plot

   First we need to get the indexes and the vectors representing the time and event.

    groups = df['group']
    T = df['time']
    E = df['event']
    ix = (groups == 'control') #indexs for the control group
   

   We then fit the control group plot first.

    kmf.fit(T[ix], E[ix], label = 'control')
    ax = kmf.plot_survival_function(color = 'blue') #blue for the control group
   

   Followed by the sick group plot.

    kmf.fit(T[~ix], E[~ix], label = 'sick') # the ~ here means negation, so NOT control group indexes
    ax = kmf.plot_survival_function(color = '#E0218A') #lets do barbie pink
   

   Optional: For better labelling. lifelines uses the matplotlib backend, so plt functions can be used as normal.

    plt.ylabel("Percent survival (%)")
    plt.xlabel("Time (AU)")
   

    plt.show()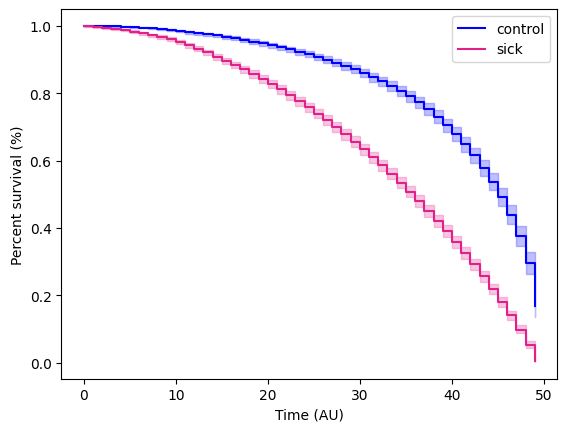
   

   

5. Statistical test

   Once finishing the KM plot, we would want to run a statistical test to see if there is a statistical difference between the two groups. In this instance, we can do a log rank test.

   First get the vectors for the two groups.

    T_control, E_control = df.loc[ix, 'time'], df.loc[ix, 'event']
    T_sick, E_sick = df.loc[~ix, 'time'], df.loc[~ix, 'event']
   

   Then run the test.

    logrank = logrank_test(T_control, T_sick, event_observed_A = E_control, event_observed_B = E_sick)
    print(logrank.p_value, logrank.test_statistic)
   

   will yield a p-value and test statistic of 5.3049732426876005e-180 and 818.4319348037003 respectively, this means that there are statistically significant difference between the control and sick group.

Reference

1. https://github.com/CamDavidsonPilon/lifelines/

back